In their recent work published in Nature Partner Journal Quantum Information, Timo Eckstein, Refik Mansuroglu, Piotr Czarnik, Jian-Xin Zhu, Michael Hartmann, Lukasz Cincio, Andrew Sornborger, and Zoë Holmes present an algorithm to simulate periodically time-dependent Hamiltonian dynamics leveraging insights from Floquet theory to be able to re-use time-independent Hamitlonian simulation algorithms.
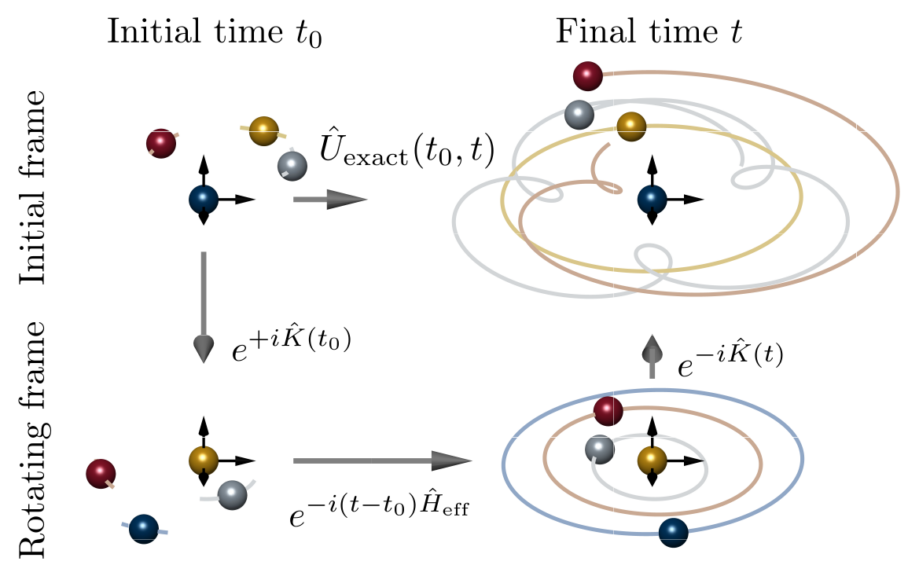
Quantum systems subject to a periodic driving field exhibit a diverse set of physical phenomena, including dynamical phase transitions and exotic non-equilibrium topological phases of matter. However, while in many cases more rewarding than their equilibrium counterparts, driven quantum systems are generally more challenging to simulate. In particular, standard Trotterization techniques are limited by significant additional time-dependent error sources; namely a time ordering as well as discrete integration error. Here, they sidestep those time-dependent errors by performing the simulation in a more natural frame of reference using a high-frequency approximation that performs a time-dependent basis transformation into a rotating frame.
They use the periodically driven biaxial next-nearest neighbour Ising (BNNNI) model, a natural test bed for quantum frustrated magnetism and criticality, as a case study to illustrate our algorithm. They implemented a 20-qubit simulation of the driven two-dimensional BNNNI model on Quantinuum’s trapped ion quantum computer. Their error analysis shows that QHiFFS exhibits not only a cubic advantage in driving frequency ω but also a linear advantage in simulation time t compared to standard Trotterization.
For more information, see their publication in Nature Partner Journal Quantum Information:
Large-scale simulations of Floquet physics on near-term quantum computers
Npj Quantum Information 10, 84 (2024)

In their recent work published in Nature Partner Journal Quantum Information, Timo Eckstein, Refik Mansuroglu, Piotr Czarnik, Jian-Xin Zhu, Michael Hartmann, Lukasz Cincio, Andrew Sornborger, and Zoë Holmes present an algorithm to simulate periodically time-dependent Hamiltonian dynamics leveraging insights from Floquet theory to be able to re-use time-independent Hamitlonian simulation algorithms.
Quantum systems subject to a periodic driving field exhibit a diverse set of physical phenomena, including dynamical phase transitions and exotic non-equilibrium topological phases of matter. However, while in many cases more rewarding than their equilibrium counterparts, driven quantum systems are generally more challenging to simulate. In particular, standard Trotterization techniques are limited by significant additional time-dependent error sources; namely a time ordering as well as discrete integration error. Here, they sidestep those time-dependent errors by performing the simulation in a more natural frame of reference using a high-frequency approximation that performs a time-dependent basis transformation into a rotating frame.
They use the periodically driven biaxial next-nearest neighbour Ising (BNNNI) model, a natural test bed for quantum frustrated magnetism and criticality, as a case study to illustrate our algorithm. They implemented a 20-qubit simulation of the driven two-dimensional BNNNI model on Quantinuum’s trapped ion quantum computer. Their error analysis shows that QHiFFS exhibits not only a cubic advantage in driving frequency ω but also a linear advantage in simulation time t compared to standard Trotterization.
For more information, see their publication in Nature Partner Journal Quantum Information:
Large-scale simulations of Floquet physics on near-term quantum computers
Npj Quantum Information 10, 84 (2024)